Sean's Blog

Sparse Distributed Representations

Modern deep learning architectures are dominated by dense embeddings. While sparse auto-encoders have gained some attention, the field lacks a clear vision for better embedding representations. In this post, I'll explore a promising alternative: Sparse Distributed Representations (SDR). This concept, popularized by Jeff Hawkins in his Hierarchical Temporal Memory (HTM) framework, draws direct inspiration from biological brains. Despite their potential advantages, SDRs have yet to gain widespread adoption in the deep learning community.

What are SDR?

SDRs are sparse matrices with spatially meaningful dimensions. The key distinction here is that the spatial arrangement of dimensions carries semantic meaning - dimensions that are spatially close represent semantically similar concepts. This property creates a natural topology in the representation space that dense embeddings typically lack.

What are the benefits of SDR over dense embeddings?

SDR vs Dense Embedding Benefits

Enhanced Interpretability

SDRs can be naturally visualized as 2D images due to their matrix structure, sparsity and spatial semantics. This makes them significantly more interpretable than dense embeddings, where the relationship between dimensions is often opaque.

Encoding Semantic Complexity

A key feature of SDRs is their ability to naturally encode single-concept versus multi-concept content:

  • Single-concept inputs (e.g., an image of a single cat or text about cats) produce spatially tightly clustered activation patterns
  • Multi-concept inputs (e.g., an image with multiple unrelated objects or text covering various topics) create more distributed activation patterns

This property provides immediate insight into the semantic complexity of the input.

Here are the top 10 average activations for a SDR trained for CLIP embeddings of CIFAR-10 images: 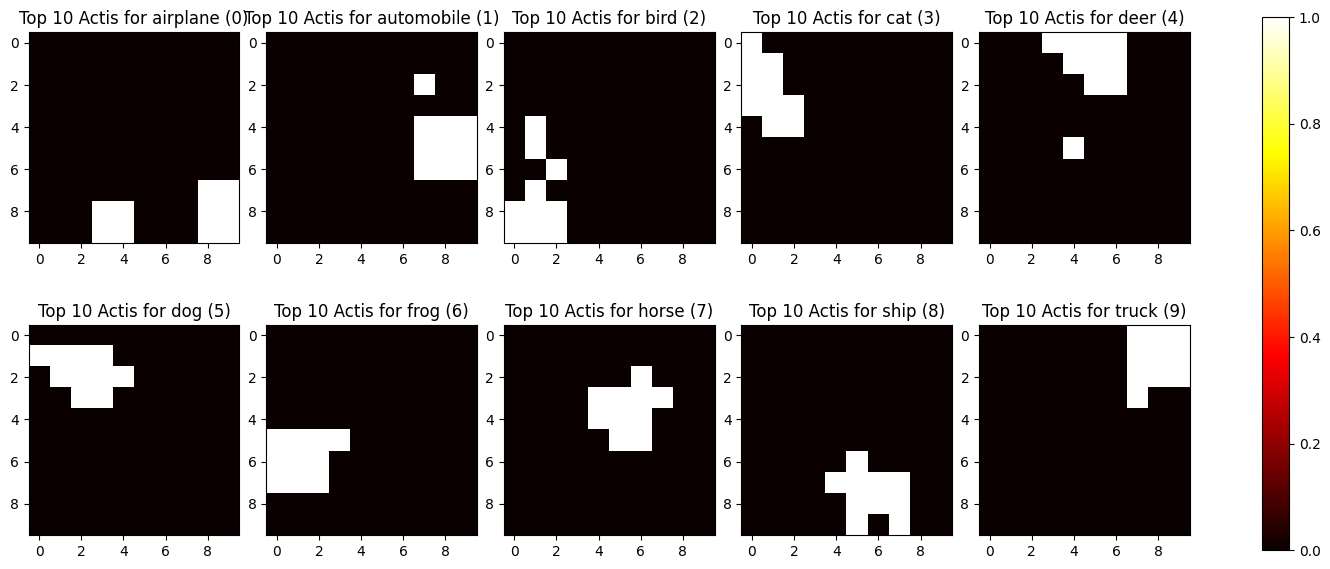cifar10-clip-som-sdr

And here a SDR for an image of a cat driving a car (multi-concept): 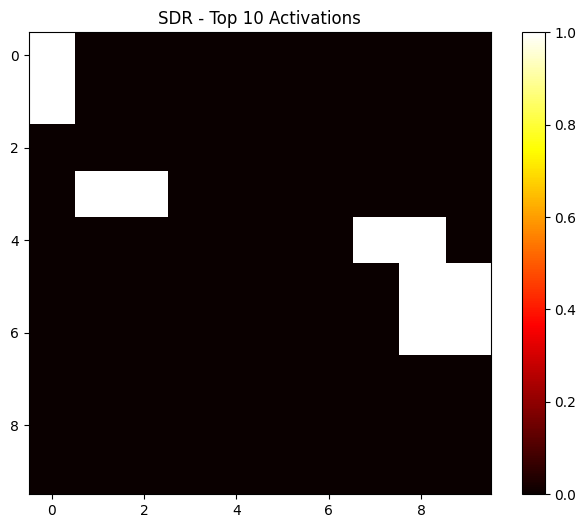multi-concept-sdr-cat-car

Built-in Novelty Detection

When presented with inputs outside the training distribution, they tend to generate highly dispersed activation patterns - even more scattered than typical multi-concept inputs. This makes outlier detection straightforward and interpretable.

Here the SDR for an image of the Pyramids (out-of-distribution): 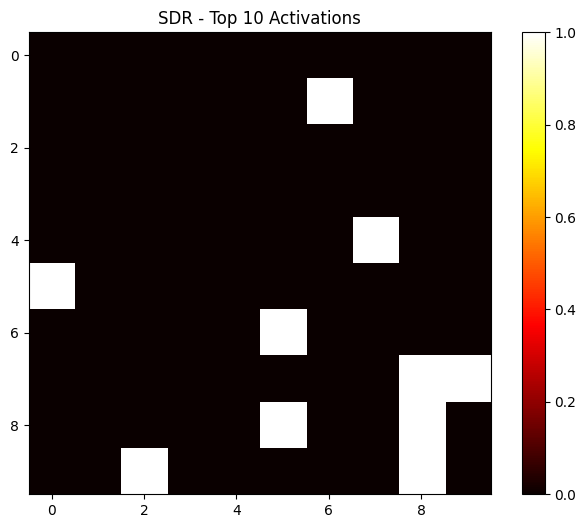ood-outlier-pyramids-sdr.png

Increased Robustness

SDRs demonstrate exceptional robustness to various types of noise and corruption:

  1. Bit Flips: Since only a small percentage of bits are active (typically 2%), random bit flips are unlikely to significantly alter the semantic meaning. Even if some active bits are flipped to inactive or vice versa, the remaining active bits still preserve most of the original information.

  2. Information Degradation: SDRs maintain semantic meaning even when a significant portion of the active bits are lost. This graceful degradation is similar to how biological neural systems maintain function despite losing neurons.

Efficient Storage + Processing

SDRs offer significant computational advantages due to their sparse nature.

Cheap Storage

Since SDRs are typically very sparse, we can store them efficiently using sparse matrix formats: Store only indices of active bits (typically 2% of dimensions).

Fast Similarity Computation

Computing similarity between SDRs is extremely efficient:

Overlap Score: Simply count shared active indices

similarity = len(set(sdr1_active_indices).intersection(set(sdr2_active_indices)))

Jaccard Similarity: Ratio of intersection to union of active bits

intersection = len(set(sdr1).intersection(set(sdr2)))
union = len(set(sdr1).union(set(sdr2)))
similarity = intersection / union

SDR Operations

SDRs support several efficient operations:

  1. Union: Combining multiple SDRs

    • Take union of active indices (bitwise OR)
    • Useful for creating composite representations
    • Maintains semantic meaning while potentially decreasing sparsity

  2. Intersection: Finding common features

    • Take intersection of active indices (bitwise AND)
    • Reveals shared semantic components
    • Results in sparser representation

How to generate SDR?

Jeff Hawkins / Numenta has not published any open-source implementation that I am aware of.

I came up with this simple implementation:

  1. Start with dense embeddings from a pre-trained model
  2. Train a Kohonen Map (SOM) on these embeddings
  3. For each input, activate only K best-matching units to create the sparse distributed representation

This approach leverages the topology-preserving properties of SOMs while enforcing sparsity through top-K selection. The resulting representations naturally exhibit the desired SDR properties.

Here is my code (Jupyter Notebook): https://github.com/SeanPedersen/SparseDistributedRepresentations

A different implemenation I found: https://github.com/dizcza/EmbedderSDR

References